Modulo e argomento di un vettore
Per calcolare la parte reale ed immaginaria di un numero complesso basta moltiplicare il valore del modulo rispettivamente per il coseno e per il seno dell' argomento.
Se invece dobbiamo determinare il modulo e l' argomento, partendo dalla forma algebrica, il calcolo è un po' più impegnativo. Difatti a ciascun valore del seno e del coseno (eccetto 1 e -1) corrispondono due angoli simmetrici; solitamente le calcolatrici restituiscono il valore più vicino alla posizione 0°, oppure il primo valore che si incontra ruotando in senso antiorario. Di seguito viene descritto il metodo degll' angolo parziale.
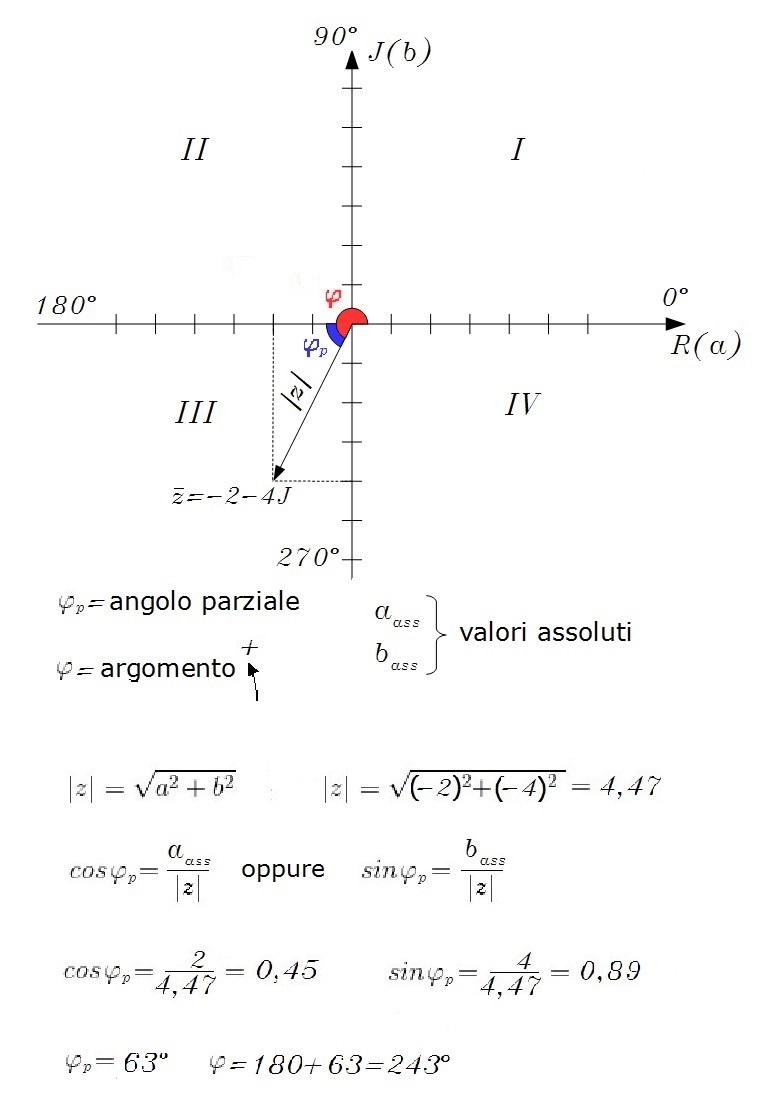
Prendiamo come esempio il numero complesso z=-2-4J. La parte reale ed immaginaria (a, b) sono entrambe negative, quindi il vettore si troverà nel III quadrante. Calcoliamo il seno oppure il coseno dell' angolo parziale, che è dato dal rapporto tra il valore assoluto della parte immaginaria o reale ed il modulo. Impostando il calcolo dell' angolo la calcolatrice restituisce un valore positivo e compreso tra 0 e 90 gradi, nel nostro caso 63°. Dato che il vettore si trova nel III quadrante, per calcolare
l' argomento in forma positiva sommiamo 63° all' angolo piatto, ottenendo 243°.
L' angolo parziale è compreso tra la semiretta su cui giace il modulo ed una semiretta dell' asse reale, positiva se il vettore si trova nei quadranti I e IV, oppure negativa se il vettore si trova nei quadranti II e III. La sua ampiezza è descritta in senso orario se il vettore si trova nei quadranti II e IV, oppure in senso antiorario se il vettore si trova nei quadranti I e III, partendo sempre dalla semiretta dell' asse reale.
Home