Vettori e numeri complessi
Le grandezze fisiche si dividono in due grandi categorie: scalari e vettoriali.
Le grandezze scalari sono definite da una semplice quantità, che può essere ad esempio la distanza tra due punti, la temperatura, il peso di un corpo.
Le grandezze vettoriali sono definite da una quantità o modulo, da una direzione e da un verso. Oltre che graficamente, i vettori possono essere rappresentati attraverso i numeri complessi.
Un numero complesso (in generale si indica con la lettera z) è praticamente un binomio formato da un termine noto che prende il nome di parte reale e da un multiplo dell' unità immaginaria; quest' ultima corrisponde alla radice quadrata di -1 (inesistente nei numeri reali) e viene solitamente indicata con la lettera J.
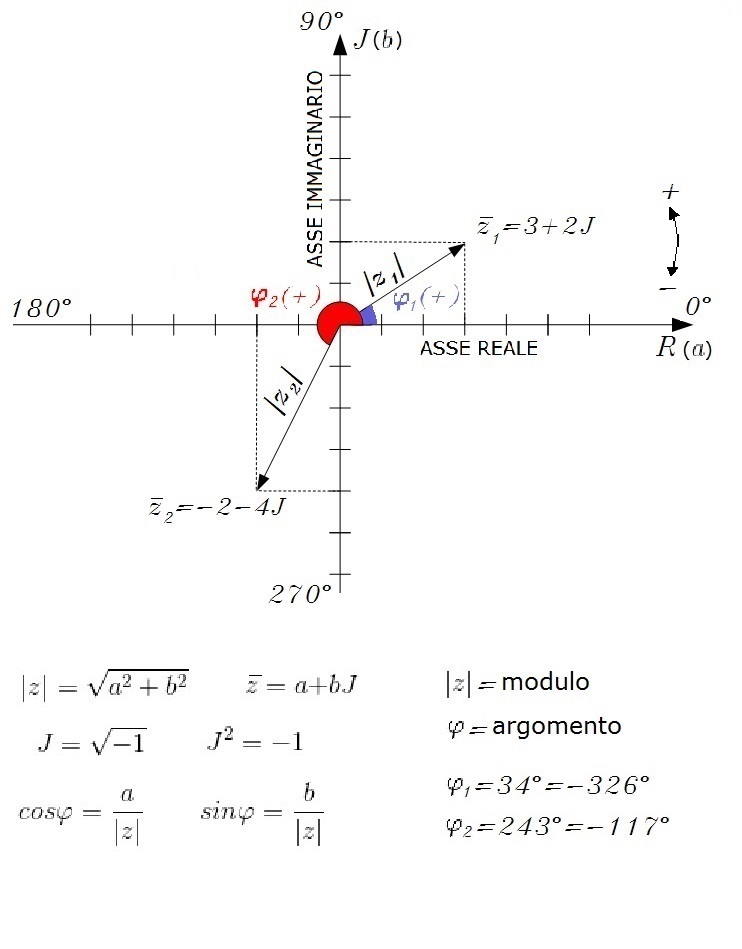
I numeri complessi si possono rappresentare su un piano cartesiano formato dai due assi reale ed immaginario. In pratica la parte reale ed immaginaria sono i cateti di un triangolo rettangolo, mentre l' ipotenusa rappresenta il modulo (senza segno). L' argomento è l' ampiezza
dell' angolo compreso tra la semiretta su cui giace il modulo e la semiretta positiva dell' asse reale, che chiameremo posizione 0°. Tale ampiezza viene presa in senso antiorario con segno positivo oppure in senso orario con segno negativo, partendo sempre dalla posizione 0°.
Per calcolare il modulo e l' argomento partendo dalla forma algebrica, oppure viceversa, si usa il teorema di Pitagora e la trigonometria.
Per le operazioni tra numeri complessi si applicano le stesse regole dei polinomi, tenendo però presente che
l' unità immaginaria elevata al quadrato corrisponde a -1.
Home